こんにちは。
少しずつ暖かい日が増え、春の訪れを感じ始めるようになりましたね。
春が近づいてくると、お花見で着ていくための春服を探すような方も多いのではないでしょうか。
一方で、防寒性の高い厚手のコートは、秋から冬にかけて購入することが多いと思います。
厚手のコートは衣類の中では高価な部類に入るので、秋から冬にかけては、一般的に衣類の消費額が大きくなるということになります。
このように、商材には季節によって売上が上下しやすいものもあります。
この季節性は、データ分析の際には障害となることもあります。
本日は季節性のある商品を分析する際のテクニック、季節調整について説明します。
目次
1. 12か月移動平均の計算方法と意義
2. 移動平均のその他の活用方法
3. 注意点
4. まとめ
1. 12か月移動平均の計算方法と意義
以下のグラフは、政府統計の総合窓口 (e-stat.go.jp)の公表している家計調査から取得したデータから作成した、二人以上の世帯が洋服にかけた消費額の推移を表したものです。
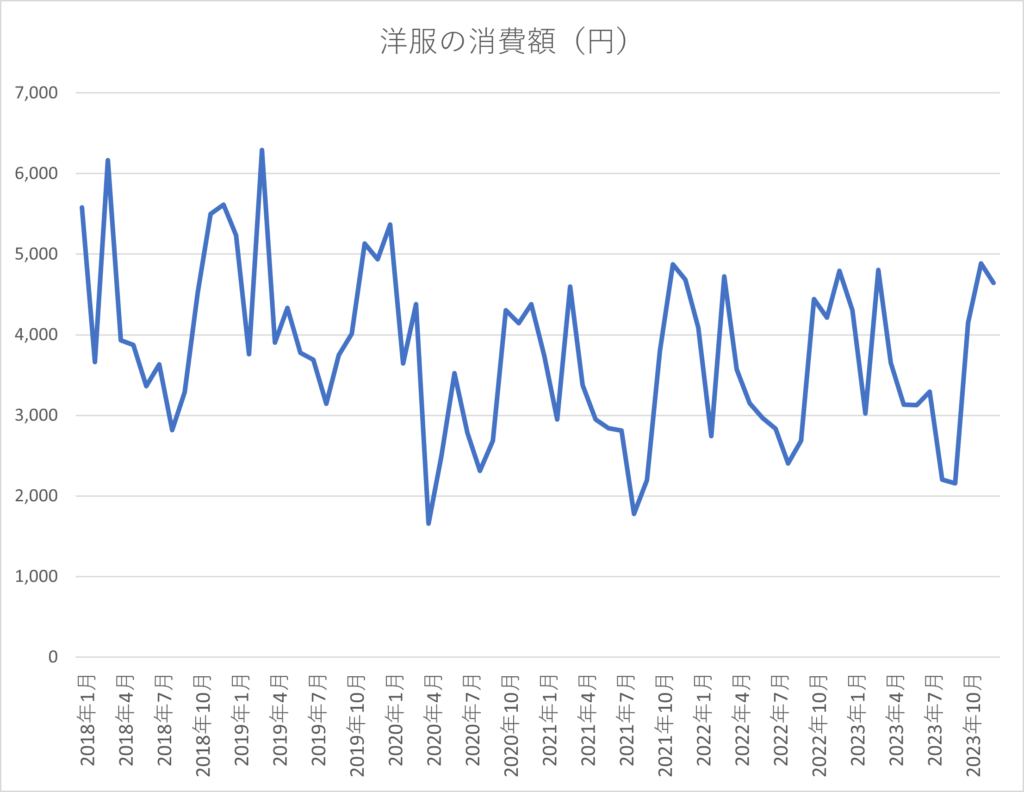
2018年1月から2023年12月までの月別のデータですが、毎年秋から冬にかけては消費額が多く、春から夏にかけては消費額が少ないようです。
これは前述の通り、冬服のほうが単価が高いことなどが影響していると思われ、ここからやはり衣類の消費額は季節によって上下しやすいことがわかります。
しかし、全体的な傾向を考えたいときはどうでしょうか。
つまり、2018年から2023年にかけて、衣類の消費額は増えているのか、減っているのか、ということを調べたい場合です。
このグラフを見ると、なんとなく右肩下がりに見えるような気もしますが、全体的に波打っているせいでわかりにくいですよね。
そこで行うべきなのが、季節調整です。
季節調整の方法はいくつかありますが、今回はその中でも簡単な、12か月移動平均を使った季節調整について説明します。
12か月移動平均の計算式は、以下です。
移動平均値=その月から12か月前までの各数値の平均値
移動平均自体にもいくつか種類はありますが、今回は後方移動平均を使用しています。
例えば、2019年12月を基準とした場合、その月の移動平均値は2019年1月から12月までの数値の平均値ということになります。
次月の2020年1月の移動平均値は、2019年2月から2020年1月までの数値の平均値、というように、1か月ずつずれた区間の平均値をとっていくこととなります。
さて、この数値を計算するメリットはどこにあるでしょうか。
ポイントは、どの月を基準とした場合でも1月から12月までの各月の数値が1度ずつ含まれることになるところにあります。
今回の洋服の消費額の場合、秋から冬にあたる各月の数値は毎年高く、春から夏にあたる各月の数値は毎年低いという傾向があります。
そこで例えば2018年11月の数値と2019年8月の数値を比べた場合、前者のほうが高いのは当たり前で、そのために、全体として消費が拡大しているのかどうかがわからないという問題がありました。
あるいはもう少し範囲を拡大して、2018年11月から2019年1月と、2019年8月から10月、のように3か月の数値を合計して比較してみても、前者は冬、後者は夏の数値ですから、前者のほうが高いのは当然です。
一方、12か月移動平均の場合、どの月を基準とした場合であっても、春から冬まで全ての季節に該当する月を合計して12で割ることになるので、各数値に季節による偏りがなくなり、季節性を排除した数値が得られることになるのです。
それでも各月の数値がだんだん増えていけば、12で割られる前の分子の部分の数値が大きくなってくるので、移動平均値もだんだん大きくなってくることとなり、全体的な傾向として上昇しているのか、下降しているのかが見えてきます。
上記のグラフに実際にオレンジ色で12か月移動平均値のグラフを追加したのが下の図です。
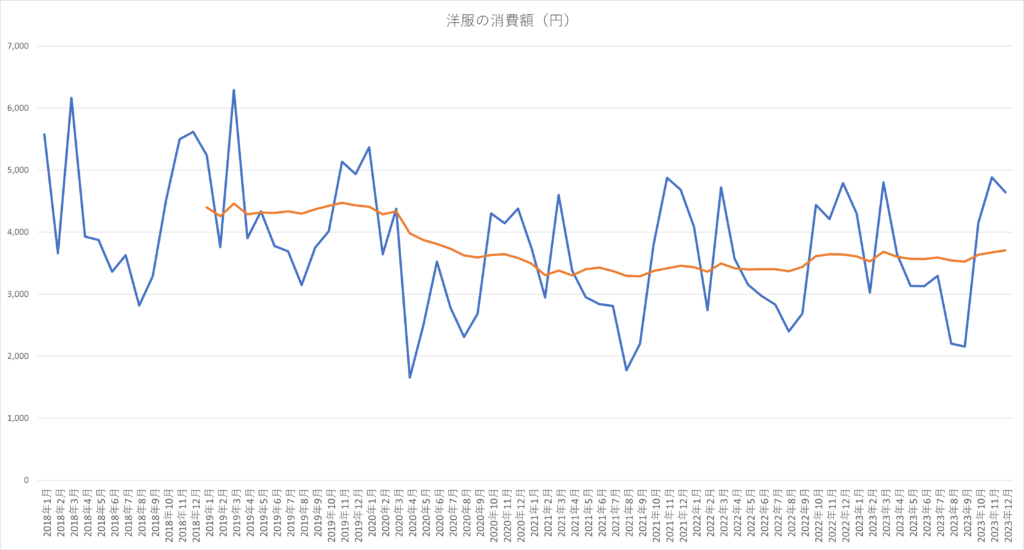
基準の月から12か月前からを参照して計算するため、移動平均値は2019年1月からしか存在しません。
これを見てみていかがでしょうか。
季節変動によって表れていた波がなくなり、全体的な傾向が見えてきましたね。
先ほどは右肩下がりに見えると言いましたが、こうして見ると、2020年初め頃から緩やかに下がってきているものの、2021年頃からはほぼ横ばいになっているようです。
むしろ、ほんの少し上向きになってきているようにすら見えます。
このように、12か月移動平均によって季節変動をなくし、全体的な傾向を見やすくすることができます。
2. 移動平均のその他の活用方法
今回は月次データの変動を調整してみましたが、移動平均は月次データ以外の分析でも利用できます。
例えば、飲食店の売上データが日次の粒度で取得できたとします。
その場合は、曜日による変動が起こりえます。
一般的には、土日や祝日のほうが売上は高い傾向があるでしょうから、純粋に平日と休日の数値を比較しても、売上の成長率は判断しにくいかもしれません。
このような場合は、7日間移動平均を計算します。
これによって各曜日の数値が平均化され、曜日による変動を無視して傾向を見ることができます。
曜日や月でなくても、あらかじめ特定の周期で波があることがわかっているデータなら、移動平均を使って波の影響をなくすことができるでしょう。
3. 注意点
このように便利な移動平均ですが、注意点もあります。
そのうちの一つが、外れ値の影響が広がってしまうことです。
例えば先ほどの飲食店の売上データの例で、ある日貸し切りパーティーの営業をする日があり、その日だけ普段の3倍ほどの売上が出たとしましょう。
当然日次データのグラフもその日だけ外れ値となりますが、7日間移動平均値はどうなるでしょうか。
その日を含むその先一週間の計算式の分子に、貸し切りパーティーの日の売上が加味されることになるので、一週間分のデータが丸々大きくなってしまいます。
売上が特別大きかったのは一日だけなのに、一週間分の売上が大きかったことように見えてしまい、こうなると全体の傾向を見るという目的から逸脱してきてしまいますよね。
このような場合には、外れ値を除外して再計算するなどの処理をすべきでしょう。
4. まとめ
いかがでしたか。
今回は移動平均と季節調整について紹介してみました。
実際にデータ分析を行う際には、本記事で触れていない注意点なども確認し、データの特性に適した分析法を使うようにしてみてください。
弊社medeluでは、このようなデータ分析も活用しながら、コンサルティングを行っています。
どうぞお気軽にご相談ください。
(関連記事)
バスケット分析とは?~データ分析手法~
ビニングでデータの特徴を捉えよう~データ分析手法~
最終更新日:2025年2月13日